Las áreas dentro de la geometría del plano-medio
Esta sección es una continuación de lo tratado en el Suplemento # 1, en donde las nociones de longitudes en el plano-medio superior de Poincaré son extendidas al concepto de superficies en ese mismo plano hiperbólico.
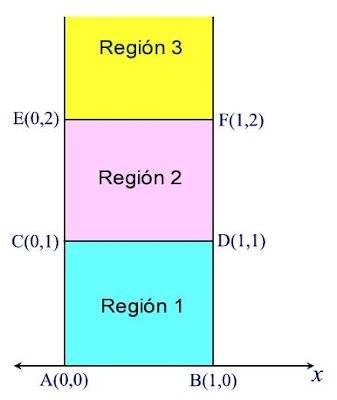
Habiendo encontrado la manera de poder asignarle un número a las longitudes medidas en el plano-medio superior, el siguiente paso es tratar de encontrar una manera para poder medir las áreas hiperbólicas limitadas dentro de cierta región del espacio. Para ello, considérese el siguiente dibujo en el cual se han levantado dos perpendiculares al eje x, con la perpendicular izquierda coincidiendo con lo que vendría siendo el eje y de un plano Cartesiano, y con tres regiones rectangulares identificadas entre dichas líneas verticales (la región 1 de color ciano, la región 2 de color rosa, y la región 3 de color amarillo, esta última extendiéndose arriba hasta el infinito):
Si estuviéramos en la geometría Euclideana, la región 1 indudablemente tendría una área de 1 metro cuadrado (o 1 centímetro cuadrado, o lo que sea según la unidad que se use para medir distancias), la región 2 también tendría una área igual al área de la región 1, mientras que la región 3, extendiéndose hacia arriba ilimitadamente, tendría una área infinitamente grande. Pero no estamos ya en el plano Euclideano, estamos en el plano hiperbólico, en donde las cosas actúan de modo distinto.
Primero obtendremos el área de la región 1 situada entre los vértices A, B, C y D, después obtendremos el área entre los vértices C, D, E y F, y por último veremos que podemos hacer con la región amarilla. Pero antes de hacer tal cosa, tenemos que encontrar alguna definición para nuestra área hiperbólica. Una extensión natural a la definición de área en la geometría plana Euclideana dentro de una región R:
inspirada en la redefinición que se había dado en el plano-medio de Poincaré para la longitud hiperbólica sería la siguiente al tratarse de una superficie limitada en una región R:
Usemos esta definición para calcular las áreas de las tres regiones señaladas en la figura de arriba. Empezaremos con el cálculo de la superficie hiperbólica Sh para la región 2:
A continuación, se calculará la superficie hiperbólica de la región 1:
Por último, se llevará a cabo el cálculo de la superficie hiperbólica de la región 3:
Las tres regiones mostradas en el ejemplo anterior no forman cada una de ellas un rectángulo en el plano-medio de Poincaré, puesto que para tener tal cosa se requiere que los dos pares de rectas paralelas que determinan a un rectángulo sean rectas hiperbólicas, las cuales deben ser líneas verticales perpendiculares al eje x o arcos de círculos centrados en el eje x, y claramente las líneas horizontales delimitando cada región no son arcos de círculo. A continuación tenemos un verdadero cuadrilátero en el plano-medio superior, con una línea media EF trazada entre las dos rectas hiperbólicas verticales:
La línea media EF es perpendicular tanto a la recta hiperbólica AB como a la recta hiperbólica CD por ser perpendicular a las tangentes que pasan por los puntos E y F. Es, en efecto, la perpendicular común a ambas paralelas AB y CD, de la cual solo puede haber una entre dos rectas paralelas hiperbólicas. Levantando la curva AB hacia arriba manteniendo el centro del círculo que la produce en el eje x, se confundirá con una recta Euclideana, y los ángulos internos en los vértices A y B serán de 90 grados, serán ángulos rectos. Será un cuadrilátero en cuya base AB (viéndolo invertido) los ángulos internos serán rectos, y en cuya cumbre los ángulos internos serán agudos. Ya hemos visto ese cuadrilátero con anterioridad. Es el cuadrilátero de Saccheri. Esto fue precisamente lo que descubrió Saccheri sin saberlo al rechazar el postulado de las paralelas de Euclides, el famoso quinto postulado.
Ahora veamos algo sobre el área de un triángulo hiperbólico en el plano-medio superior.
Ya habíamos visto anteriormente que en la geometría hiperbólica el área dentro de un triángulo se mide no en base a lo que midan los lados de un triángulo sino en base a lo que miden sus ángulos internos, en base a lo que le falta a la suma de dichos ángulos para ser 180 grados, lo que llamamos defecto del triángulo. Ahora veamos cuál es el triángulo de la mayor área posible que podamos trazar en una geometría hiperbólica. Ya habíamos visto que en la geometría hiperbólica el área de un triángulo depende no de las longitudes de los lados que definen al triángulo sino de las magnitudes de los ángulos internos del triángulo, y habíamos visto que dicha área estaba dada por el defecto del triángulo δ, definido como lo que le falta a la suma de los ángulos internos del triángulo hiperbólico para dar 180 grados (medidos en radianes). Entonces el triángulo con la mayor área posible será aquél con el mayor defecto posible, lo cual ocurrirá cuando la suma de los ángulos internos del triángulo sea cero. Esto a primera vista podrá parecerle a algunos como una afirmación temeraria, dado que si la suma de los ángulos internos se vuelve cero entonces más que tener un triángulo conteniendo la mayor cantidad posible de área tendremos un triángulo que habrá desaparecido de nuestra vista. Sin embargo, esto no es así, y hay que recordar nuevamente que tenemos que ajustar nuestro modo de pensar a lo que ocurre en una geometría radicalmente diferente a la geometría Euclideana. A continuación se muestra un triángulo hiperbólico ABC en el medio-plano de Poincaré delimitado por las rectas k, l y m, cuyos tres ángulos internos tienen un valor de cero (el ángulo se mide trazando tangentes a las rectas hiperbólicas en cada punto de contacto):
No nos debe quedar ninguna duda de que este es un triángulo hiperbólico válido. Sus tres lados son rectas hiperbólicas, son arcos de circunferencia obtenidas haciendo centro en el eje x.
Aquí no terminan las sorpresas. Si trazamos un triángulo hiperbólico de modo tal que dos de sus lados sean líneas verticales sobre el plano-medio de Poincaré (esto lo podemos obtener empezando con un triángulo hiperbólico "típico", aumentando enormemente los radios de definen a dos de sus rectas de modo tal que terminen confundiéndose con dos líneas verticales levantadas en el plano-medio), tendremos lo que se llama un triángulo asintótico como el que se muestra a continuación:
Y resulta que este triángulo ¡tiene un área finita! Nuevamente, tenemos que adecuar nuestra manera de pensar para poder entender esto. El ángulo en el vértice A será de 90 grados (pi/2 radianes), mientras que el ángulo en el vértice B será de cero grados. Y el tercer vértice, el que no podemos ver porque está arriba, muy arriba, en "el infinito", tendrá un valor de cero grados (esto lo podemos ver trazando un arco de círculo centrado en el eje x que pase por el vértice A y se cruce con la recta vertical que pasa por el punto B, con lo cual tendremos el tercer lado de un triángulo "usual". Al ir aumentando el radio que corresponde a este tercer lado el ángulo del vértice que forma dicho arco con la recta vertical que pasa por el punto B irá disminuyendo hasta que, en la cercanía del infinito, el ángulo será de cero grados, y tendremos justo lo que muestra la figura de arriba. Puesto que el área de un triángulo hiperbólico está definida por el defecto del triángulo δ, el área de este triángulo asintótico será:
δ = π - (π/2 + 0 + 0)
δ = área del triángulo asintótico = π/2
δ = área del triángulo asintótico = π/2
Entonces el triángulo asintótico mostrado arriba tiene un área finita de π/2 unidades hiperbólicas.
Movimiento de figuras en el plano hiperbólico
En la geometría Euclideana, se supone que los cuerpos ideales son completamente rígidos y que el espacio "plano" es homogéneo e isotrópico (conservando igual todas sus características) en cualquier dirección, razón por la cual el desplazamiento de una figura geométrica de una región a otra deja dicha figura intacta, inalterada en sus dimensiones. Sin embargo, esto no es lo que ocurre en el plano-medio superior de Poincaré, en donde conforme una figura se va alejando verticalmente de la línea límite x la figura se va haciendo cada vez más grande sin límite, y en donde conforme una figura se va aproximando verticalmente a la línea límite la figura se va haciendo cada vez más pequeña.
Un movimiento de una figura en el plano puede visualizarse de dos maneras completamente equivalentes (las dos versiones son conocidas como alias y alibi), ya sea manteniendo todo el plano fijo y moviendo la figura en un sentido, o manteniendo la figura fija y moviendo todo el plano en el sentido opuesto. Supóngase que todos los puntos del plano-medio superior se desplazan de tal manera que la longitud hiperbólica de cualquier arco perteneciente a este plano-medio (semiplano) es igual a la longitud hiperbólica del mismo arco en su nueva posición. Semejante desplazamiento de los puntos lo llamaremos movimiento hiperbólico. Este concepto es análogo al concepto del movimiento del plano Euclideano, por ejemplo, al giro del plano Euclideano en cierto ángulo alrededor de cualquier punto de dicho plano. Si el movimiento hiperbólico transforma a la figura F en F', entonces las figuras F y F' se denominan figuras hiperbólicamente iguales. Veamos a continuación los dos tipos más simples de movimiento hiperbólico.
En el primer tipo de movimiento, si se traspasa cada punto del plano-medio superior en una misma distancia y en una misma dirección paralelamente a la línea límite x, resulta que cada figura se transforma en otra hiperbólicamente igual a ella. Pues no varía ni su magnitud Euclideana ni la distancia de sus puntos a x. Este tipo de movimiento lo tenemos representado en el siguiente dibujo en donde el objeto es desplazado hacia la derecha (o lo que es lo mismo, el plano-medio superior es desplazado completo hacia la izquierda):
Así pues, si el objeto recibe un movimiento de traslación estrictamente horizontal, entonces en virtud de que la relación definida en el Suplemento # 1 aplicada para cada segmento infinitesimal los segmentos de los que consta en el objeto se mantendrán a la misma distancia y de la línea límite x, entonces la integración se volverá trivial manteniendo el mismo valor para cada segmento infinitesimal del objeto.
En el segundo tipo de movimiento, el objeto es desplazado no sólo horizontalmente sino también verticalmente, manteniéndose una relación de similitud que en la siguiente figura:
transforma el segmento PQ en el segmento P'Q'. Designemos como se muestra arriba y e y', respectivamente, las distancias de los puntos Q y Q' a la línea límite x. Entonces por la semejanza de los triángulos OAQ' y OBQ, tendremos:
Por otro lado, por la semejanza de los triángulos OP'Q y OPQ, tenemos:
Se deduce que durante dicha transformación no varía la longitud hiperbólica de una línea cualesquiera cuando se lleva a cabo en la forma arriba mostrada.
El modelo Beltrami-Klein
La geometría basada en el modelo Beltrami-Klein (conocido también como el modelo Klein, el modelo proyectivo, el modelo Cayley-Klein, el disco de Klein, etc.) se obtiene deformando la geometría hiperbólica del disco de Poincaré de modo tal que las rectas hiperbólicas en el disco de Poincaré (arcos de circunferencia) terminan convertidos en cuerdas, en una manera como se muestra a continuación:
De este modo, el arco AB se convierte en la cuerda AB, y el arco CD se convierte en la cuerda CD. Al igual que el disco de inversión y el medio-plano de Poincaré, el modelo de Klein también es un modelo de espacio hiperbólico.
A primera vista, el modelo de Klein parece similar al disco de Poincaré, pero no lo es, ya que los habitantes de un modelo de Klein ven las líneas rectas en su espacio tal y como las vemos nosotros desde fuera. Las geodésicas dentro del modelo de Klein son cuerdas Euclideanas de un disco unitario. Sin embargo, sus mediciones angulares serán diferentes a las nuestras. Un modelo de este tipo en el que la forma de medir los ángulos internos es diferente a como lo hacemos nosotros es llamado no-conformal. Una forma simplista pero válida de ver el modelo de Klein es considerando que, en cierta forma, las geodésicas del disco de Poincaré, las cuales son todas ellas arcos de circunferencia, son "enderezadas" proyectándolas hacia las cuerdas que tocan los puntos extremos de las geodésicas.
A continuación tenemos la comparación de varias rectas trazadas en los tres modelos que hemos visto, el modelo de Klein, el disco de Poincaré, y el plano-medio superior:
Dado un disco de Poincaré que contenga figuras geométricas, dichas figuras pueden ser proyectadas hacia sus equivalentes en un disco de Klein y viceversa, pero esto involucra varios pasos que deben ser comprendidos antes de que se lleve a cabo dicha transformación. Para tener una idea sobre cómo es posible el poder llevar a cabo una transformación de este tipo, se hará un bosquejo que, aunque no exacto y sobresimplificado, demostrará como tal cosa puede ser posible.
Primero que nada, podemos empezar tomando un disco de Klein, el cual se supone de radio unitario, y empezar ampliando dicho radio hasta hacerlo infinitamente grande, manteniéndonos en todo momento en el "centro" del disco. Esto tendrá el efecto de convertir al disco de Klein en lo que para nosotros parecerá un plano infinitamente grande sin "borde" circular exterior. Hecho esto, podemos tomar un hemisferio, de radio unitario, reposando su polo sobre el centro del "plano de Klein". Por último, tomamos el disco de Poincaré y lo alineamos por encima del área transveral del hemisferio, y como el disco de Poincaré es también unitario, podemos llevar a cabo una alineación matemáticamente perfecta como se muestra a continuación:
El disco # 1 mostrado arriba puede tomarse como el disco de Poincaré, y el disco # 2 puede tomarse como el disco de Klein en el momento en que empieza a ser "estirado" radialmente hacia el infinito. Hecho esto, podemos trazar una recta Euclideana sobre el "plano Klein", y a continuación podemos ir trazando rayos desde dicha recta hacia el centro de simetría del hemisferio, marcando los puntos de dichos rayos que tocan la superficie esférica del hemisferio:
Ahora se demostrará que toda recta l como la que se muestra arriba al ser proyectada sobre la superficie de un hemisferio H se convertirá en un arco de círculo. Considérense varios puntos de la recta l hacia la superficie del hemisferio. Los rayos de la proyección de la recta que van hacia el centro de simetría O del hemisferio H forman parte todos ellos de un plano que atraviesa al hemisferio. Y como un plano que atraviesa una esfera pasando por su centro de simetría divide a la esfera en dos partes iguales, formará entonces un círculo máximo en la superficie de la esfera, o en este caso del hemisferio. Entonces la línea k será un arco de círculo. Por último, podemos proyectar hacia arriba, hacia la tapa del hemisferio, hacia el disco de Poincaré, cada uno de los puntos que forman al arco k. En la siguiente figura, que representa un corte transversal lateral del hemisferio, podemos ver varios puntos llegados originalmente del disco # 2 proyectados hacia el disco # 1 (se ha destacado el punto P cuya imagen termina siendo el punto P'):
Así, al proyectar cada uno de los puntos que forman parte del arco k hacia arriba sobre el disco que forma la tapa del hemisferio se obtendrá un segmento de línea en el disco de Poincaré que corresponde a la recta Euclideana que le fue proyectada desde el modelo Klein. Este tipo de transformaciones constituyen lo que en matemáticas llamamos un isomorfismo, a cada punto en el disco # 1 corresponde un punto en el disco # 2, y viceversa; hay una correspondencia de uno a uno, una correspondencia biunívoca.
Sin embargo, como ya se dijo, lo que se ha llevado a cabo arriba es una sobresimplificación del asunto con fines pedagógicos. Entendiblemente, no hay muchos textos de matemáticas, inclusive a nivel de licenciatura universitaria, que entren a fondo en los detalles sobre la demostración requerida para poder obtener las imágenes en el disco hiperbólico de Poincaré el equivalente de las rectas Euclideanas de un disco de Klein. Sin embargo, el resultado matemático final, las fórmulas necesarias para llevar a cabo las transformaciones, es fácil de digerir. El uso de las fórmulas que serán presentadas aquí está basado en el uso de las coordenadas polares (r,θ):
en lugar de coordenadas Cartesianas (x,y). Con esto, podemos llevar a cabo la conversión punto por punto de una figura geométrica de un disco a otro mediante las siguientes fórmulas para la conversión Klein-Poincaré:
mientras que para la conversión Poincaré-Klein utilizamos las siguientes fórmulas: